Parallel lines cut by a transversal worksheet with answers pdf
The Parallel lines cut by a transversal worksheet designed to aid students in recognizing and understanding various angle relationships formed by parallel lines intersected by a transversal. By exploring corresponding angles, alternate interior angles, consecutive Interior Angles and alternate exterior angles, students will develop a comprehensive understanding of the relationships between these angles.
You can download Parallel lines cut by a transversal worksheet from the following links:
- Two Parallel Lines Cut by a Transversal By StudyWinner.com
- Parallel Lines and Transversals By Kuta Software – Infinite Geometry
- Parallel Lines Cut by a Transversal By Amazing Mathematics
- Parallel Lines Cut by a Transversal By Darlene Walstrum, Patrick Henry High School
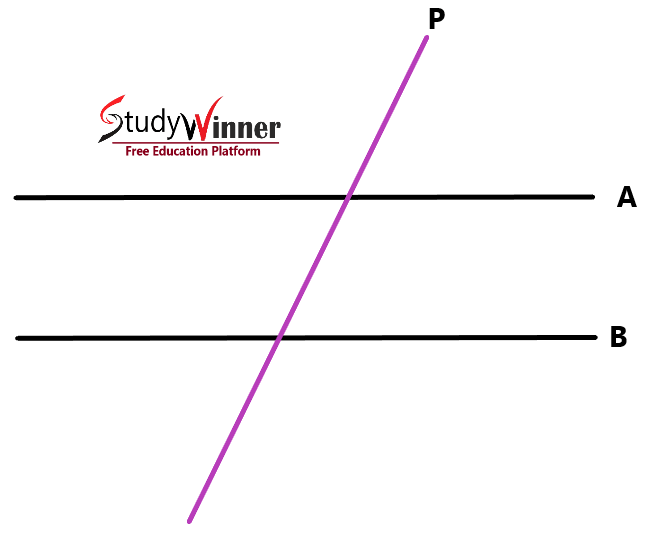
Which diagram shows parallel lines cut by a transversal ?
In below diagram, There are two parallel lines, Line A and Line B. Transversal is a Line (P) that intersects Line A and Line B.
Parallel Lines and Transversals
Certainly, parallel lines and transversals are fundamental concepts in geometry. When two lines are parallel, they maintain a constant distance between them and never intersect, regardless of their extended length. A transversal is a line that intersects two or more other lines.
Key angle relationships that arise when a transversal intersects parallel lines include:
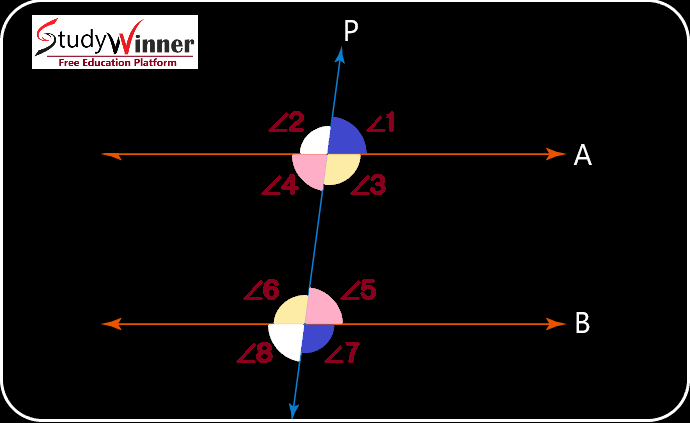
- Corresponding Angles: These are angles that occupy the same relative position at the intersection of the transversal with two parallel lines. Corresponding angles are congruent, meaning they have the same measure.
- Alternate Interior Angles: These angles lie on opposite sides of the transversal and inside the two parallel lines. They are also congruent.
- Alternate Exterior Angles: These angles lie on opposite sides of the transversal and outside the two parallel lines. Like alternate interior angles, they are congruent.
- Consecutive (Same-Side) Interior Angles: These angles are on the same side of the transversal and inside the parallel lines. They are supplementary, meaning their measures add up to 180 degrees.
- Vertical Angles: These angles formed by intersecting lines and are opposite each other. Vertical angles are always congruent.
Understanding these relationships helps in problem-solving involving geometric figures formed by parallel lines and transversals. Students often use these relationships to determine unknown angles by setting up and solving equations based on the properties of these angles.
Parallel lines cut by a transversal worksheet Key Objectives
- Identification of Angle Types: Students will learn to identify various angle types that form when a transversal intersects parallel lines, including corresponding angles, vertical angles, alternate interior angles, and alternate exterior angles.
- Angle Relationships: Understanding the properties of these angles will help students recognize patterns and relationships between angle pairs, including congruence, supplementary angles, and relationships based on parallel lines and transversals.
- Problem-Solving Skills: Utilizing the knowledge of angle relationships, students will practice setting up and solving equations to find missing angle measures within the geometric configurations formed by parallel lines and transversals.
FAQs
A. The theorem that describes the relationships between angles formed by the intersection of two parallel lines with a transversal is the Corresponding Angles Theorem.
Corresponding angles are congruent: Angles that occupy the same relative position at each intersection (one on each parallel line) are congruent. For instance, if a transversal intersects two parallel lines and creates angles at the top left and top right corners, those angles will be congruent.
A. Corresponding angles are congruent.
A. When parallel lines are cut by a transversal, several angle relationships emerge: Corresponding Angles, Alternate Interior Angles, Alternate Exterior Angles, Consecutive (Same-Side) Interior Angles and Vertical Angles.
A. Corresponding Angles, Alternate Interior Angles, Alternate Exterior Angles, Consecutive (Same-Side) Interior Angles
A. A transversal is a line that intersects two or more other lines at distinct points. When a transversal intersects two parallel lines, it forms several angles with those lines, leading to specific angle relationships.